MESH - A Journey Through Discrete Geometry
By Beau Janzen and Konrad Polthier
 A Mathematical Video on Discrete Curves and Surfaces and Their
Role in Geometry, Numerics and Computer Graphics
A Mathematical Video on Discrete Curves and Surfaces and Their
Role in Geometry, Numerics and Computer Graphics
Abstract: MESH is a groundbreaking computer animation that explores the advancement of discrete geometry from the ancient Greeks to contemporary research topics that have never previously been visualized. With its synthesis of cutting-edge visualization, breathtaking artistry, storytelling and humor, Mesh presents complex ideas in a way that is palpable and relevant to even a novice audience. Along the journey, we encounter applications ranging from crystals and computer graphics to wine barrels and soap bubbles, and bring to life concepts such as the Schwarz lantern, Gauss curvature, surface optimization and engineering, and minimal surfaces.
The film is completely computer-generated using the latest technology and spans the range from ancient Greek mathematics to the area of geometric modelling of today. MESH has already won several science awards worldwide. The authors are Konrad Polthier, a professor of mathematics, and Beau Janzen, a professional film director.
The film is an excellent teaching tool for courses on geometry, visualization, scientific computing and geometric modeling at universities and centers for computational science, and can also be used in schools.
Awards and Reviews: MESH received numerous international awards and press attention:
- Festival awards (Scinema, Red Stick, New York, ...)
- Press reviews (Welt, c't magazin, Deutschlandfunk et al.)
Order: Published by Springer Video in the series "VideoMATH" and available at following sites:
- vismath: DVD-Deutsch (Deutsch plus English track) Previews available
- Springer: DVD-Deutsch, DVD-English (German and English editions)
Citation: MESH - a journey through discrete geometry, Beau Janzen and Konrad Polthier; DVD, Springer Verlag 2006
Bits from the Script ... |
|
|
From an ancient Etruscan site outside of Padua, archaeologists unearthed a mysterious stone. Dating from before 500 BC, the stone was carved with an amazing symmetry. It had twelve identical faces. Each face was made of five edges of the same length and five angles of the same size. And, each face was rotated from its adjoining faces by the same angle. The symmetry and harmony of this stone could be no accident - but why would someone craft such an object? What would draw someone to even conceive of such a thing? Although the purpose of the stone is shrouded in mystery, perhaps the inspiration for carving it came from observing how nature itself constructs shapes in rocks ..." |
|
|
Greek Philosophy: "... Plato himself didn't use the name "Platonic Solids" that we use today, but called them the "cosmic bodies". Because of the perfect beauty he saw in them, he reasoned that these regular solids represented the four elements - the building blocks of all matter. He believed that the tetrahedron represented fire, the cube represented earth, the icosahedron represented water, and the octahedron represented air. Representing the universe, or the fifth element, "quintessence" was the dodecahedron ..." |
|
|
Crystals: "... The shape of crystals is determined by their atomic building blocks. In a grain of everyday table salt, we can see a crystal that looks like a cube. The molecules that form salt consist of one sodium atom joined to one chlorine atom. When these molecules pack themselves together, they are able to fit perfectly next to one another like puzzle pieces. The way the molecules assemble creates no gaps between them so they fill the least amount of space. The repeated pattern forms a particular structure. When we see the shape of a salt crystal, we are looking at the resulting pattern of billions of molecules packed together. This is just one pattern in the many ways in which crystals can form ..." |
|
|
Discrete Measures: "... Traditionally, winemakers simply guessed. They picked a radius for the barrel, somewhere in the middle, and estimated that the barrel's volume was a cylinder with that radius ..." "... Kepler wasn't the only one who measured complicated curving shapes by breaking them into pieces that were shrinking to zero in size. Cavalieri created similar ways of breaking things into infinitesimally small parts and summing up the pieces. Eventually, to better accomplish this task, calculus was created independently by the mathematicians Newton and Leibniz ..." |
|
|
Numerics: Finite Elements: "... Computers, with all their power, can only think about objects in terms of finite sets of numbers. The infinite number of data points on a curve can't all be crammed into a computer, no matter how large its memory. This means that computers must work in discrete terms. With the new tool of the computer, engineers could construct a building in the digital world, and test to see how structurally sound it was without the expense and danger of testing it in the real world. The problem was that computers can't handle so much data at once, and only deal with a small, finite number of points. Therefore, engineers had to resurrect the discrete way of describing the world ..." |
|
|
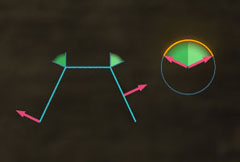
Geometry: Discrete Curvature: "... If we increase the number of edges in the polygon, we create more angles. At each of these points, the perpendicular arrow sweeps out a smaller angle. Even though there are more angles, the total sum that they sweep is the same. As the number of edges grows larger, the shape begins to look smoother, yet the total curvature remains unchanged. If we increase to an infinite number of faces on the polygon, we now have a continuously curving shape. Now, there are no more individual angles to add together, but we still know how the curvature will work. The discrete model tells us that even as points on the curved shape are moved about, the overall curvature will remain the same. From the discrete shape, we were able to learn something about the properties of the smooth shape ..." |
|
|
Computer Graphics - Scanning and Smoothing: "... A 3D computer scanner can locate a point on an object in 3D space. When a scanner samples points all over an object, the points can be assembled together into a mesh, providing a complete digital model of the object. However, there is a certain level of imperfection in the scanning process so that tiny errors are made in locating each point. Since the points are no longer part of a physical object but just mathematical points in space, we can use mathematical tools to smooth them out ..." "... To do this, we need to find the areas in the model that hold more curvature. Seeing curvature in terms of tension, we find places that have high tension and know that they are defining an edge or a corner. In areas that hold little curvature, we sample all the edges around a point equally. In areas that hold high curvature, our smoothing should average only the lengths of edges that run along the curvature, and not in opposite directions that would result in smoothing out a corner ..." |
|
|
Discrete Geometry: "... Discrete surfaces see the world in terms of specific bits of data. When mathematicians first conceived of calculus, it was a way that they could overcome the shortcomings provided by the limited view of discrete meshes. However, they soon found that calculus itself had limitations. And, ultimately, they found that, often, the best solution is to return to the simplicity and harmony of discrete meshes ..." |
|
Technical Data:
Images and Trailers
Further Information
|